Överskott vad som är. Innebörden av begreppet

2024 Författare: Henry Conors | [email protected]. Senast ändrad: 2024-02-12 13:02

Artikeln beskriver statistikens roll som vetenskap. Begreppet kurtosis och dess användning inom vetenskapen övervägs.

Statistik. Grundläggande koncept

Statistik är den grundläggande derivatan av matematisk vetenskap. Detta ämne tillhör ett antal samhällsdiscipliner som syftar till att bilda en bild av världsbilden och en kompetent analys av händelser hos elever.

Statistik studerar alla typer av processer och händelser i människors liv, lyfter fram deras mönster och presenterar allt i form av korta statistiska rapporter. Sådan vetenskap är soci alt användbar och kräver ständiga förbättringar. Överskott - vad är det? Detta är ett grundläggande koncept i grafisk statistik som hjälper till att bestämma korrektheten av perfekt kalkyl. Kurtosis bör inte ha en stark avvikelse.

Statistik låter dig tillfredsställa människors behov av tillförlitlig information om ett visst fenomen, händelse och så vidare. Att bestämma dynamiken i livsfaktorer, deras nedgång, stagnation eller tillväxt - det är precis vad denna vetenskap gör.

I den moderna världen upptar statistik en av de viktigaste platserna på den vetenskapliga arenan. Låt oss överväga begreppet "kurtosis". Vad är ett statistiskt mål och observation? Var tillämpas dessa begrepp? Läs mer om allt detta iartikel.

Vad är kurtosis i statistik?

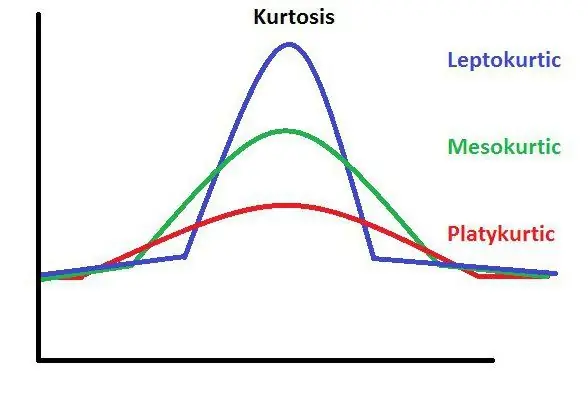
Kurtosis är ett statistiskt koncept som representerar skärpan för varje topp i en distributionsgraf. Det finns en speciell formel för dess exakta beräkning.

Expectation säger att för en jämnare fördelning av statistiska data måste kurtosis vara lika med ett positivt tal. Bokstavligen betyder detta begrepp en viss avvikelse från normen och ytterligare onormal utveckling eller funktion av det statistiska systemet.

Överdrivet uttryck av kurtos på en statistisk graf kan indikera en felaktig studie eller fel i grafens ursprungliga data. Ett sådant begrepp är skalärt till sin natur, vilket innebär att den slutliga beräkningen bör resultera i ett tal som inte kommer att innehålla variabler eller hjälpfunktioner. Så här ser kurtosis ut.

Vad är symmetrisk och asymmetrisk fördelning

Kurtosis, som är relaterad till fördelningen av den symmetriska typen, är lika med noll. Detta kan tydligt visas med en graf. Den asymmetriska grafen visar ett tal som inte är noll. Så här betecknas kurtosis.

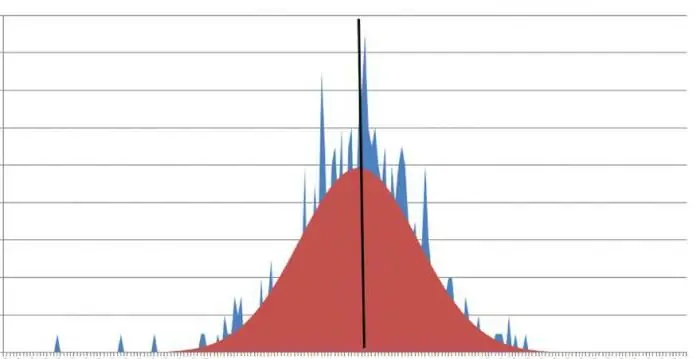
Vad är skärpan på en topp? En graf som har skarpa toppar indikerar att kurtosisvärdet är ett tal mindre än noll. Ofta finns det situationer då ett givet begrepp inte kan uttryckas med ett separat värde. I det här fallet närmar det sig minus eller plus oändlighet.